Despite the fact that not even light can escape a black hole, they do exhibit some observable features. This post will go through the properties of a black hole, and an overview of the four metrics used to describe them.

Just to note: Although I am quite knowledgeable in astrophysics and cosmology, my knowledge of black holes is not as extensive as other areas. If there’s anything I should  tweak, please let me know!

The No Hair Theorem/Information Loss Paradox

First things first: Black holes are featureless and indistinguishable from each other in every way EXCEPT mass, charge and angular momentum. This is known as the No-hair theorem.

These are the only three properties of a black hole, and are visible from the outside. However, we can only observe the present properties, as black holes don’t show any information of initial or previous conditions.

In addition, mass that falls in gets evenly distributed around the horizon, so we don’t have any information about what has fallen in a black hole.

Essentially, black holes have very little information to offer us. This is known as the black hole information loss paradox, and is a pain for those who want to observe them!

The Four Metrics

So we know there are three features of a black hole: mass, charge, and angular momentum. Can we use these to model a black hole?

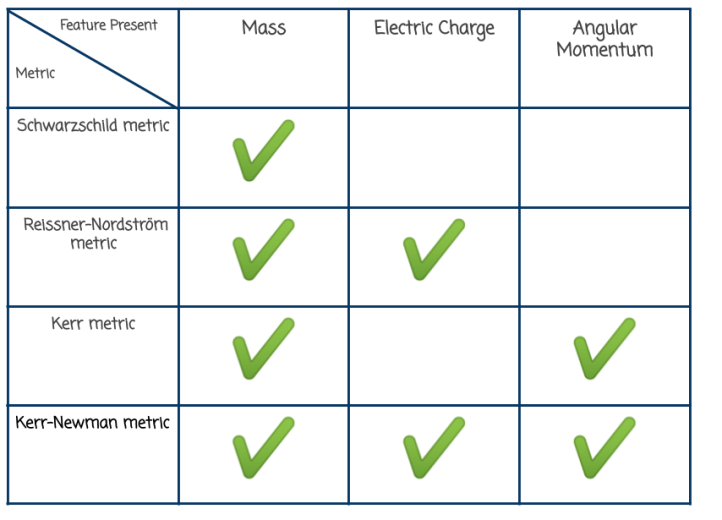
There are four metrics, each can be used to describe the gravitational fields of black holes depending what features they do and don’t have.

Here’s a handy table of them. You’ll notice that all the metrics include mass. It would be hard to imagine a massless black hole!

The Schwarzschild Metric

The Schwarzschild metric is used for black holes with NO charge and NO angular momentum. The metric provides a very good approximation for things with nearly no charge and angular momentum, such as our Sun and Earth.

The Schwarzschild radius (where the event horizon is) of a black hole is calculated using this formula:

This metric shows the singularity of a black hole to be in the very centre, and stable circular orbits can only be made 3 times away from the Schwarzschild radius. Once you get closer to the black hole, about 1.5 times the Schwarzschild radius, the gravitational strength is so high that you’re screwed.

The Schwarzschild metric provides two solutions for a singularity: the event horizon (a fake singularity), and the true singularity. When you sub in the radius of the event horizon and the radius of the singularity into the metric, you end up dividing by zero in both cases. Mathematically, this is illegal, and the true singularity is the one in the centre of the black hole.

Reissner-Nordström Metric

The Reissner-Nordström metric is used for charged non-rotating black holes. This type of black hole has an inner horizon, called the Cauchy horizon. Here events no longer happen chronologically, as things in the past can’t cause any future events. It’s a bizzare idea, which I am still yet to fully understand.

The Kerr Metric

The Kerr metric is used for rotating chargeless black holes, and with it come some stellar (pun intended) physics!

Just like spinning stars, a Kerr black hole with have a slight bulge at the equator, with more mass around this area than at the poles. The rotation will also supposedly change the shape of the singularity, causing it to be ring shaped. A Kerr black hole also has an inner Cauchy horizon.

The Kerr-Newman Metric

And lastly, the Kerr-Newman metric! This is used to model rotating charged black holes (given that the charge and angular momentum are small), but provides a very general solution and doesn’t accurately describe other situations like stars. The accretion of mass onto a black hole is also not included, so this model is quite incomplete!

 

Featured Image Credit: NASA, ESA, and D. Coe, J. Anderson, and R. van der Marel (STScI)